Les isolants topologiques sont des matériaux bien étranges : leur intérieur ne laisse pas passer le courant électrique, mais leurs surfaces sont très conductrices. Mais ce n’est pas tout. Leur conductivité de surface est vraiment spéciale. D’une part, elle n’est pas du tout affectée par les imperfections de surface, contrairement à ce que l’on observe sur les surfaces et interfaces des matériaux conventionnels tels que les hétéro-structures semi-conductrices. En effet, la conductivité de surface d’un isolant topologique résulte de l’agencement atomique dans le volume du matériau. D’autre part, la conductivité de surface d’un isolant topologique est hautement sélective en spin, ce qui a dernièrement entraîné l’excitation de la communauté de la physique de la matière condensée. Une excitation justifiée par le potentiel élevé des isolants topologiques dans de nouvelles applications comme l’information quantique, les générateurs de spin dans les circuits spintroniques, ou des composants cruciaux des nanodispositifs optoélectroniques.
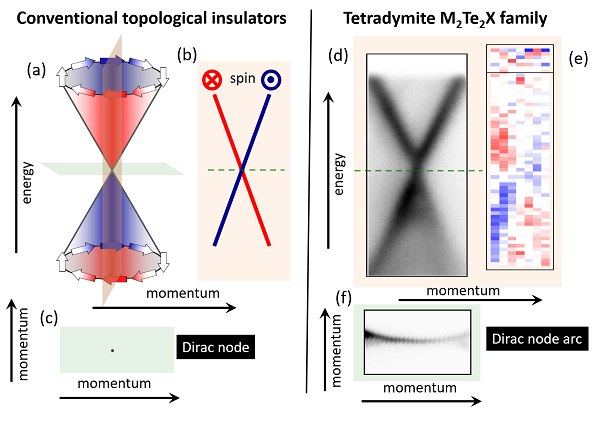
Les propriétés topologiques d’un matériau se reflètent dans sa structure de bandes électronique, qui est la relation entre l’énergie et la quantité de mouvement des électrons à l’intérieur du matériau lui-même. Le type le plus simple de comportement topologique donne naissance à deux branches d’états d’électrons qui forment un cône dans l’espace énergie-impulsion, comme montré sur la figure 1 (a). C’est ce qu’on appelle un cône de Dirac, du nom de Paul Dirac qui a d’abord trouvé ce type de comportement pour la description quantique des électrons d’une manière compatible avec la relativité d’Einstein. D’une certaine manière donc, les électrons d’un cône de Dirac à l’intérieur d’un solide sont comme des photons dans l’espace libre : ils se comportent tous les deux comme des particules sans masse ! Les électrons d’un cône de Dirac sont aussi polarisés en spin, avec des vecteurs de spin tournant autour de la surface du cône, comme le montrent les figures 1 (b, c). Il y a cependant un seul point de spin zéro (Figure 1c), le point de croisement des parties supérieure et inférieure du cône, connu sous le nom de nœud de Dirac. L’observation expérimentale d’un cône de Dirac, d’un nœud de Dirac, et d’une polarisation de spin, sont toutes des preuves irréfutables du comportement topologique à la surface d’un matériau.
En utilisant une technique expérimentale qui nous permet d’avoir une vision directe de la structure de bandes et des spins électroniques, nous avons étudié une nouvelle famille de matériaux de formule chimique générale M2Te2X (M = Ti ou Zr, ou Hf et X = P ou As) . Nous avons observé expérimentalement un cône de Dirac [panneau (d)], et montré que ses électrons sont polarisés en spin [panneau (e)]. Avons-nous observé un nœud Dirac ? Ici, la réponse est d’autant plus intéressante que nous avons pu montrer qu’au lieu d’un nœud de Dirac conventionnel, la structure de bande électronique forme des « lignes nodales de Dirac » le long de certaines directions de haute symétrie de la structure cristalline [panneau (f)]. En fait, ces lignes nodales de Dirac représentent des électrons de masse infinie, c’est-à-dire, des électrons essentiellement localisés dans le solide ! Ainsi, les électrons des états topologiques dans ces matériaux sont sans masse lorsqu’ils se déplacent dans une direction, et fortement massifs dans la direction perpendiculaire. Par conséquent, cette classe de matériaux est un candidat de choix pour une conduction topologique hautement anisotrope.
Publication : Ji Dai et al., Experimental Observation and Spin Texture of Dirac Node Arcs in Tetradymite Topological Metals. Phys. Rev. Lett. 126, 196407 (2021).
Contact :